
De ontdekking van irrationale getallen kwam van een sekte
Werd een wiskundige verdronken door leden van een vreemde sekte? Veel mythen en legenden draaien om de geschiedenis van irrationale getallen.
Hij werd met de dood bestraft voor zijn ontdekking van irrationele getallen - dat is tenminste de legende rond de oude geleerde Hippasos van Metapont. Wat er daadwerkelijk gebeurde in de 5e eeuw voor Christus is tot op de dag van vandaag onduidelijk.
Hippasus behoorde blijkbaar tot de Pythagoreeërs, een sekte die zich onder andere richtte op wiskunde en getallenmystiek. Een kernelement van hun leer had betrekking op harmonische getalsverhoudingen, waaronder breuken van gehele getallen. Vanuit het perspectief van die tijd kon de hele wereld worden beschreven met behulp van natuurlijke en rationele getallen. Toen Hippasos echter de lengteverhoudingen van een pentagram - het symbool van de Pythagoreeërs - onderzocht, realiseerde hij zich dat sommige zijlengtes niet als breuken konden worden uitgedrukt.
Dit was het eerste gedocumenteerde bewijs van het bestaan van irrationele getallen. Volgens sommige verhalen namen de Pythagoreeërs hier aanstoot aan, omdat zulke getallen in strijd waren met hun wereldbeeld. In andere interpretaties had Hippasos zijn resultaat gepubliceerd en daarmee de geheimhoudingsbepalingen van het verbond geschonden. Hoe dan ook, Hippasos verdronk blijkbaar in zee na zijn ontdekking. Soms wordt gemeld dat de Pythagoreeërs hem van een schip gooiden nadat hij hen had geïnformeerd over zijn ontdekking - of dat zijn dood een ongeluk was, maar de Pythagoreeërs beschouwden het als een straf van God. De huidige interpretaties gaan ervan uit dat niets van dit alles waar is. Integendeel: de ontdekking van Hippasus werd toen al erkend als een wiskundige doorbraak waar de Pythagoreeërs trots op waren - op voorwaarde dat het bewijs ook echt van Hippasus kwam. Want zelfs dat is niet zeker.
Het enige dat is overgeleverd is dat de Pythagoreeërs de incommensurabiliteit van bepaalde grootheden bewezen, waaruit het bestaan van irrationele getallen volgt. De Pythagoreeërs zelf zijn ook het onderwerp van een aantal verhalen, waarvan de waarheidsgetrouwheid vaak twijfelachtig is. De gemeenschap werd waarschijnlijk gesticht in wat nu Zuid-Italië is door Pythagoras van Samos - de Griekse geleerde naar wie de beroemde stelling van Pythagoras is vernoemd (hoewel het onduidelijk is of hij de stelling ook echt heeft bewezen).
De Pythagoreeërs zelf zijn ook het onderwerp van een aantal verhalen, waarvan de juistheid vaak in twijfel wordt getrokken.
De Pythagoreeërs verwierpen rijkdom en leefden vegetarisch en ascetisch. Ze geloofden ook in reïncarnatie, wat hen onderscheidde van de rest van de Griekse bevolking in de oudheid. Naast wiskunde hield de gemeenschap zich waarschijnlijk ook bezig met filosofie en politiek. Hun standpunten waren echter niet erg populair en daarom werden ze vervolgd: Er waren verschillende aanvallen op de gemeenschap; een paar decennia na de dood van Pythagoras verdween de liga volledig.
Getallen buiten breuken
Hoewel veel over de Pythagoreeërs mysterieus blijft, worden zij algemeen beschouwd als de ontdekkers van irrationele getallen. We leren nu op school dat er waarden zijn die niet kunnen worden uitgedrukt als het quotiënt van twee gehele getallen. Dit besef lijkt echter helemaal niet zo natuurlijk: alle irrationale waarden kunnen immers precies benaderd worden door breuken - ook al is dat bij sommige irrationale getallen moeilijker dan bij andere.
Het bewijs van Hippasus (of een andere Pythagoras) is het gemakkelijkst te illustreren met een gelijkbenige en rechthoekige driehoek, ook al werd het oorspronkelijke bewijs waarschijnlijk uitgevoerd op een andere meetkundige figuur (waarschijnlijk de vijfhoek). De twee katheten van lengte a in een gelijkbenige rechthoekige driehoek vormen dus een rechte hoek, waartegenover de hypotenusa van lengte c ligt.
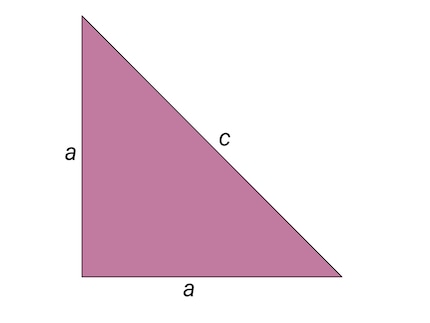
Bron: © Spektrum der Wissenschaft / Manon Bischoff (detail)
Zo'n driehoek heeft een vaste hoogte-breedteverhouding a⁄c. Als a en c rationale getallen zijn, kunnen de lengtes van de zijden van de driehoek zo gekozen worden dat a en c overeenkomen met de kleinst mogelijke natuurlijke getallen (dat wil zeggen dat ze geen gemeenschappelijke delers hebben). Als de hoogte-breedteverhouding bijvoorbeeld ⅔ is, dan zou je a = 2 en c = 3 kiezen. Dit betekent: aangenomen dat de lengtes van de driehoek overeenkomen met rationale getallen, zijn a en c gehele getallen en hebben ze geen gemeenschappelijke delers.
Een bewijs van tegenspraak
Hippasos gebruikte dit feit om een tegenspraak te creëren - en zo te bewijzen dat de oorspronkelijke aanname fout moet zijn. Ten eerste gebruikte hij de stelling van Pythagoras om de lengte van de schuine zijde c uit te drukken als functie van de twee katheten a: 2a2 = c2. Omdat a en c gehele getallen zijn, volgt uit de vorige vergelijking dat c2 een even getal moet zijn. Bijgevolg is c ook deelbaar door twee: c = 2n, waarbij n een natuurlijk getal is.
Toevoeging van c = 2n aan de oorspronkelijke vergelijking levert op: 2a2 = (2n)2 = 4n2. Deze twee kunnen aan beide kanten worden gereduceerd, wat het volgende resultaat oplevert: a2 = 2n2. Omdat a ook een geheel getal is, volgt hieruit dat a2 en dus ook a even getallen zijn. Dit is echter in tegenspraak met de oorspronkelijke aanname; want als a en c allebei even zijn, kunnen ze geen delers zijn.
This allowed Hippasos to conclude that the aspect ratio of an isosceles right-angled triangle a⁄c cannot correspond to a rational number. Met andere woorden, er zijn getallen die niet kunnen worden weergegeven als de verhouding van twee gehele getallen. Als je bijvoorbeeld de lengtes van de twee zijden van de driehoek a = 1 kiest, dan is c = √2. En zoals we nu weten is √2 een irrationaal getal. Zijn decimalen gaan oneindig door zonder zich ooit te herhalen.
Vanuit het perspectief van vandaag lijkt het bestaan van irrationele waarden niet zo verrassend, omdat we er al op jonge leeftijd mee geconfronteerd worden. Het is moeilijk in te schatten welk effect een dergelijk besef zo'n 2500 jaar geleden moet hebben gehad. In ieder geval moet het het wiskundige wereldbeeld op zijn kop hebben gezet. Geen wonder dat er zoveel mythen en legenden over deze ontdekking bestaan.
Spectrum van de wetenschap
Wij zijn partners van Spektrum der Wissenschaft en willen gefundeerde informatie toegankelijker voor je maken. Volg Spektrum der Wissenschaft als je de artikelen leuk vindt.
Oorspronkelijk artikel op Spektrum.de
Deskundigen uit wetenschap en onderzoek doen verslag van de huidige bevindingen op hun gebied - deskundig, authentiek en begrijpelijk.
Van de nieuwe iPhone tot de wederopstanding van de mode uit de jaren 80. De redactie categoriseert.
Alles tonen